Limit ve Süreklilik Konu Anlatımı ve Ders Notları

LİMİT ve SÜREKLİLİK

I. LİMİT

A. SOLDAN YAKLAŞMA, SAĞDAN YAKLAŞMA

x değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşmaya soldan yaklaşma denir ve 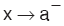biçiminde gösterilir.

x değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa, bu tür yaklaşmaya sağdan yaklaşma denir ve 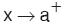biçiminde gösterilir.

B. LİMİT KAVRAMI

Limit kavramını bir fonksiyonun grafiği üzerinde açıklayalım:

Grafiği verilen y = f(x) fonksiyonu için, apsisleri; x = a nın solunda yer alan ve giderek a ya yaklaşan A(x₁, y₄) , B(x₂, y₃) , C(x₃, y₂) , D(x₄, y₁), … noktalarını göz önüne alalım:

Bu noktaların apsisleri olan x₁, x₂, x₃, x₄, … giderek a ya yaklaşırken, ordinatları

f(x₁) = y₄, f(x₂) = y₃, f(x₃) = y₂, f(x₄) = y₁, … giderek b ye yaklaşır.

Bu durumu; x, a ya soldan yaklaşıyorken f(x) b ye yaklaşır şeklinde ifade edebiliriz. Bu durumda,

f(x) in x = a daki soldan limiti b dir denir. Ve

şeklinde gösterilir.

Yukarıdakine benzer şekilde, apsisleri x = a nın sağında yer alan ve giderek a ya yaklaşan

E(x₈, y₅) , F(x₇, y₆) , G(x₆, y₇) , H(x₅, y₈) , … noktalarını göz önüne alalım.

Bu noktaların apsisleri olan x₈, x₇ , x₆ , x₅ , … giderek a ya yaklaşırken, ordinatlar f(x₈) = y₅ , f(x₇) = y_{6 ,} f(x₆) = y₇ , f(x₅) = y₈ , … giderek d ye yaklaşır.

Bu durumu “x, a ya sağdan yaklaşıyorken f(x) d ye yaklaşır.” şeklinde ifade edebiliriz.

Bu durumda; f(x) in x = a daki sağdan limiti d dir denir. Ve

biçiminde gösterilir.

Kural

f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit ise fonksiyonun x = a da limiti vardır ve x in a noktasındaki limiti L ise, biçiminde gösterilir. x = a daki sağ limit ve sol limit değeri, fonksiyonun x = a daki limitidir. f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit değil ise fonksiyonun x = a da limiti yoktur.

C. UÇ NOKTALARDAKİ LİMİT

f fonksiyonu [a, b) aralığından [c, d) aralığına tanımlı olduğu için, uç noktalardaki limitleri araştırılırken, sadece tanımlı olduğu tarafın limitine bakılarak sonuca gidilir.

Fonksiyonun bir noktada limitinin olması için, o noktada tanımlı olması zorunlu değildir. Buna göre,

Kural

D. LİMİTLE İLGİLİ ÖZELLİKLER

Özellik

f ve g , x = a da limitleri olan iki fonksiyon olsun.

Özellik

Özellik

Özellik

Özellik

Özellik

E. PARÇALI FONKSİYONUN LİMİTİ

Özellik

F. İŞARET FONKSİYONUNUN LİMİTİ

Özellik

f(x) = sgn [g(x)] olsun. Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır. Söz gelimi, f(x) = sgn(x2) fonksiyonunun x = 0 da limiti vardır ve 1 dir.

G. TAM DEĞER FONKSİYONUNUN LİMİTİ

Özellik

Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır. Söz gelimi, fonksiyonunun x = 0 da limiti vardır.

H. NİN x = a DAKİ LİMİTİ

Özellik

I. TRİGONOMETRİK  FONKSİYONLARIN LİMİTİ

1. sinx in ve cosx in limiti

sinx ve cosx fonksiyonu bütün x reel değerleri için tanımlı olduğu için,

olur.

2. tanx in limiti

tanx fonksiyonu olmak üzere,

koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,

olur.

Sonuç

3. cotx in limiti

cotx fonksiyonu olmak üzere, koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,

olur.

Sonuç

J. BELİRSİZLİK DURUMLARI

belirsizlikleriyle karşılaştığımızda aşağıda verilen yöntemler kullanılarak limit hesaplanır. Bu limitler türevin içinde vereceğimiz L’Hospital kuralıyla da hesaplanabilir.

Kural

Kural

m, n Î N olmak üzere, olur.

Kural

a > 0 olmak üzere, ¥ – ¥ belirsizliği olan limitler, kuralını kullanarak hesaplanabilir.

Kural

Buna göre, 0 × ¥ belirsizliği veya belirsizliğine dönüştürülerek sonuca gidilir.

Kural

II. SÜREKLİLİK

Kural

f(x) fonksiyonu apsisi x = a olan noktada süreklidir.

Sonuç

y = f(x) fonksiyonu x = a da sürekli ise,

Uyarı

f(x) fonksiyonu apsisi x = a olan noktada sürekli değil ise, süreksizdir.

Kural

1. Bir fonksiyon bir noktada tanımsız ise, o noktada süreksizdir. 2. Bir fonksiyon bir noktada limitsiz ise, o noktada süreksizdir. 3. Bir fonksiyon bir noktada tanımlı ve limitli ancak, tanım değeri limit değerinden farklı ise, bu noktada süreksizdir.