Üçgende Bağıntılar Video Ders Olarak İzlemek İçin Tıklayın
Kenar Orta Dikmeleri – Çevrel Çember Video Ders Olarak İzlemek İçin Tıklayın
ÜÇGENDE AÇIORTAY BAĞINTILARI
1. Açıortay
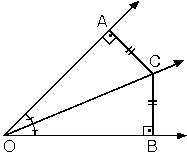
| Herhangi bir açının ölçüsünü iki eş açıya bölen ışınlara açıortay denir.Yandaki şekilde AOB açısını iki eş açıya ayıran [OC ışınına açıortay denir. | 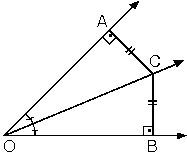 |
Açıortay üzerindeki herhangi bir noktadan açının kenarlarına çizilen dik uzunluklar eşittir.
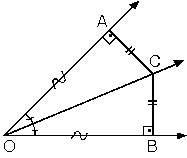
AOB bir açı,
[OC açıortay
m(AOC) = m(COB)
AOC ve BOC eş üçgenler olduğundan |OA| = |OB| |
 |
2. İç Açıortay Bağıntısı
ABC üçgeninde [AN] açıortay ABN ve ANC üçgenlerinin[BC] tabanına göre, yükseklikleri eşit olduğundan
|
 |
ABN üçgeninde [AB] kenarına ait yükseklik ANC üçgeninde[AC] kenarına ait yüksekliğe eşittir.
|
 |
[AN] açıortay olmak şartıyla bu iki alan oranını birleştirirsek; (1) ve (2) den
 |
olur |
ABC üçgeninde [AN] açıortay olmak şartıyla
|
 |
3. İç Açıortay Uzunluğu
| ABC üçgeninde A köşesinden çizdiğimiz açıortayuzunluğuna nAdersek
|
 |
4. Dış Açıortay Bağıntısı
ABC üçgeninde [AD], A köşesine ait dış açıortaydır.
|
 |
5. Dış Açıortay Uzunluğu
| ABC üçgeninde [AD] dış açıortayının uzunluğunan’Adersek
|
 |
6. İç açıortayla dış açıortay arasındaki açı
| m(DAE)=90° |  |
ABC üçgeninde [AD] iç açıortayı ile [AE] dış açıortayı arasındaki açı için
2a + 2b = 180°
a + b = 90° dir.
| [DA] ^ [AE] |
|
 |
- ÜÇGENDE KENARORTAY BAĞINTILARI
1. Ağırlık Merkezi
Üçgenlerde kenarortaylar bir noktada kesişirler.Kenarortayların kesişim noktasına ağırlık merkezi denir.
| ABC üçgeninde [AD], [BE] ve [CF] kenarortaylarınınkesiştikleri G noktasına ABC üçgeninin ağırlık merkezidenir. |  |
a. Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim olacak şekilde böler.
ABC üçgeninde D, E, F noktaları bulundukları kenarlarınorta noktaları ve G ağırlık merkezi ise
|
 |
| b. Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir. |  |
| c. ABC üçgeninde [AD] kenarortay ve|AG| = 2|GD| olduğundan G noktasıağırlık merkezidir. |  |
| d. ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG|olduğundan G noktası ağırlık merkezidir. |  |
| e.ABC üçgeninde|AG| = 2|GD| ve |CG| = 2|GF|eşitliğini sağlayan G noktası ABC
üçgeninin ağırlık merkezidir. |
 |
2. Dik üçgende hipotenüse ait kenarortay hipotenüsün yarısına eşittir.
ABC dik üçgeninde [BD] hipotenüse ait kenarortay
|
 |
3. Kenarortayların Böldüğü Alanlar
| a.Kenarortaylar üçgenin alanını altı eşit parçaya bölerler. |  |
| b.G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür. |  |
| c. G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür. |  |
| 4.ABC üçgeninde kenarortaylar ve [FE] çizilirse|AK| = 3x|KG| = x
|GD| = 2x eşitlikleri bulunur. |
 |
K noktası [AD] kenarortayının orta noktasıdır.
|
|
| a. ABC üçgeninde kenarortaylar ve [FE] çizildiğindeşekildeki gibi bir alan bölünmesi oluşur. |  |
| b.Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür. |  |
5. Kenarortay Uzunluğu
| ABC üçgeninde A köşesinden çizilenkenarortayın uzunluğuna Vadersek
Bu bağıntı diğer kenarortaylar içinde geçerlidir. |
 |
Kenarortaylar taraf tarafa toplanırsa

Kenarortaylar taraf tarafa toplanırsa
![]()
6. Dik Üçgende Kenarortaylar
| A açısı 90° olan bir dik üçgende kenarortaylar arasında
|
 |
gerçekten muazzam
Canım ya aklım karışıktı iyice karıştı
ben çok beğendim. özellikle formüllerin olması sınav öncesi sağlam bir tekrar için iyi oldu teşekkürler.
Üçgen formülleri çok işime yaradı sınav öncesi ilaç gibi geldi teşekkürler.
abi çözümlü soru lazım saçmalamayınız
Bu ne ya çok saçma hem bilgi az hem de yanlış bilgiler var
Hayır hiç de yanlış bilgi yok sen bilmiyorsan o senin sorunun
Katılıyorum.
bunasıl sorular sbs ye girsem hep si yanlış cıkar
Doğru diyon kardeşim bu ne ya