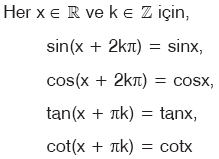
TRİGONOMETRİ 2
I. PERİYODİK FONKSİYONLAR
f, A kümesinden B kümesine tanımlı bir fonksiyon olsun.
f : A ® B
Her x Î A için f(x + T) = f(x)
olacak şekilde sıfırdan farklı en az bir T reel sayısı varsa; f fonksiyonuna periyodik fonksiyon, T ¹ 0 reel sayısına f nin periyodu denir. Bu eşitliği gerçekleyen birden fazla T reel sayısı varsa, bunların pozitif olanlarının en küçüğüne f fonksiyonunun esas periyodu denir.
f(x) in esas periyodu T ise, k tam sayı olmak üzere,
f(x) in periyodu k × T dir.
TRİGONOMETRİK FONKSİYONLARIN PERİYOTLARI
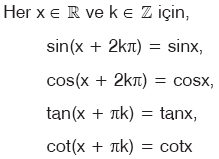
olduğu için sinx, cosx, tanx ve cotx fonksiyonları periyodiktir.
sinx ve cosx fonksiyonlarının periyodu 2kp, tanx ve cotx fonksiyonlarının periyodu kp dir.
sinx ve cosx fonksiyonlarının esas periyodu (k = 1 için) 2p; tanx ve cotx fonksiyonlarının esas periyodu p dir.
Kural
| a, b, c, d birer reel sayı ve m pozitif tam sayı olmak üzere,
f(x) = a + b × sinm(cx + d) g(x) = a + b × cosm(cx + d) fonksiyonlarının esas periyotları T olsun. Bu durumda,
olur. |
Kural
| a, b, c, d birer reel sayı ve m pozitif tam sayı olmak üzere,
f(x) = a + b × tanm(cx + d) g(x) = a + b × cotm(cx + d) fonksiyonlarının esas periyotları T olsun. Bu durumda,
|
Kural

fonksiyonlarının esas periyodu, g(x) ve h(x) fonksiyonlarının esas periyotlarının en küçük ortak katına (e.k.o.k. una) eşittir. |
Uyarı

Buradaki kesirleri en sade biçimde olmalıdır. |
Uyarı
| f(x) = h(x) × g(x) olmak üzere, f(x) in esas periyodu, h(x) ve g(x) fonksiyonlarının esas periyotlarının en küçük ortak katına (e.k.o.k. una) eşit olmayabilir.
Eğer, f(x) = h(x) × g(x) in esas periyodu bulunacaksa, f(x) i fonksiyonların toplamı biçiminde yazarız. Sonrada toplanan fonksiyonların esas periyotlarının en küçük ortak katı alınır. Yukarıdaki açıklamalar bölünen fonksiyonlar için de geçerlidir. |
II. TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ
Trigonometrik fonksiyonların grafikleri çizilirken,
1. Fonksiyonun esas periyodu bulunur.
2. Bulunan periyoda uygun bir aralık seçilir.
3. Seçilen aralıkta fonksiyonun değişim tablosu yapılır. Bunun için, fonksiyonun bazı özel reel sayılarda alacağı değerlerin tablosu yapılır. Tabloda fonksiyonun aldığı değer bir sonraki aldığı değerden küçük ise (aldığı değer artmış ise) o aralığa  sembolünü yazarız. Eğer, fonksiyonun aldığı değer bir sonraki aldığı değerden büyük ise (aldığı değer azalmış ise) o aralığa
sembolünü yazarız. Eğer, fonksiyonun aldığı değer bir sonraki aldığı değerden büyük ise (aldığı değer azalmış ise) o aralığa  sembolünü yazarız.
sembolünü yazarız.
4. Seçilen bir periyotluk aralıkta fonksiyonun grafiği çizilir. Oluşan grafik, fonksiyonun periyodu aralığında tekrarlanacağı unutulmamalıdır.
A. SİNÜS FONKSİYONUNUN GRAFİĞİ

fonksiyonunun grafiği aşağıda çizilmiştir.

B. KOSİNÜS FONKSİYONUNUN GRAFİĞİ

fonksiyonunun grafiği aşağıda çizilmiştir.

Sonuç
  fonksiyonu bire bir ve fonksiyonu bire bir ve
örtendir.
örtendir. |
C. TANJANT FONKSİYONUNUN GRAFİĞİ

fonksiyonunun grafiği kesiksiz olarak çizilmiştir.

D. KOTANJANT FONKSİYONUNUN GRAFİĞİ

fonksiyonunun grafiği kesiksiz olarak çizilmiştir.

Sonuç
  fonksiyonu bire bir ve fonksiyonu bire bir ve
örtendir.
|
III. TERS TRİGONOMETRİK FONKSİYONLAR
A. ARKSİNÜS FONKSİYONU
f(x) = sinx fonksiyonunun tanım aralığı  alınırsa bu fonksiyon bire bir ve örten olur.
alınırsa bu fonksiyon bire bir ve örten olur.
Bu durumda,

fonksiyonunun tersi,
f–1(x) = sin–1x veya f–1(x) = arcsinx
şeklinde gösterilir ve

B. ARKKOSİNÜS FONKSİYONU
f(x) = cosx fonksiyonunun tanım aralığı
[0, p] alınırsa bu fonksiyon bire bir ve örten olur. Bu durumda,
f : [0, p] ® [–1, 1]
f(x) = cosx
fonksiyonunun tersi,
f–1(x) = cos–1x veya f–1(x) = arccosx
şeklinde gösterilir ve
arccos : [–1, 1] ® [0, p] dir.
C. ARKTANJANT FONKSİYONU
f(x) = tanx fonksiyonunun tanım aralığı
 alınırsa bu fonksiyon bire bir ve örten olur.
alınırsa bu fonksiyon bire bir ve örten olur.
Bu durumda,

fonksiyonunun tersi,
f–1(x) = tan–1x veya f–1(x) = arctanx
şeklinde gösterilir ve

D. ARKKOTANJANT FONKSİYONU

fonksiyonu bire bir ve örtendir.

fonksiyonuna cotx in ters fonksiyonu denir. Kotanjant fonksiyonunun tersi,

şeklinde gösterilir.
Sonuç
| Bir fonksiyonun ters fonksiyonunun ters fonksiyonu fonksiyonun kendisine eşittir.
|
Sonuç
 q = arcsinx ise, x = sinq dır. q = arcsinx ise, x = sinq dır.
|
IV. ÜÇGENDE TRİGONOMETRİK BAĞINTILAR
A. SİNÜS TEOREMİ
Kural
| Bir ABC üçgeninin kenar uzunlukları a, b, c; çevrel çemberinin yarıçapı R birim olmak üzere,
|
B. KOSİNÜS TEOREMİ
Kural
| Bir ABC üçgeninin kenar uzunlukları; a, b, c olmak üzere,
a2 = b2 + c2 – 2 × b × c × cosA dır. b2 = a2 + c2 – 2 × a × c × cosB dir. c2 = a2 + b2 – 2 × a × b × cosC dir. |
C. ÜÇGENİN ALANI
Sonuç
| Bir ABC üçgeninin kenar uzunlukları; a, b, c olmak üzere,
|
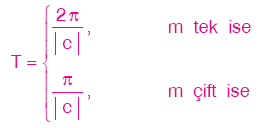
Açıklayıcı olmuş teşekkürler
””””””””””””Uyarı
f(x) = h(x) × g(x) olmak üzere, f(x) in esas periyodu, h(x) ve g(x) fonksiyonlarının esas periyotlarının en küçük ortak katına (e.k.o.k. una) eşit olmayabilir.
Eğer, f(x) = h(x) × g(x) in esas periyodu bulunacaksa, f(x) i fonksiyonların toplamı biçiminde yazarız. Sonrada toplanan fonksiyonların esas periyotlarının en küçük ortak katı alınır.
Yukarıdaki açıklamalar bölünen fonksiyonlar için de geçerlidir.””””””””””’
burda benim anlamadığım f(x) fonksiyonun toplamı biçiminde yazmak nasıl olur bir örnekle açıklarmısınız….
trigonometri konu anlarımları için LİSEGO.com dan bakabilirsin.
Trigonometri konu anlatımları için LİSEGO’ya bakabilirsin, çok faydasını gördüm.
çok sağolun ….