Polinomlar Konu Anlatımı ve Ders Notları

POLİNOMLAR

A. POLİNOMLAR

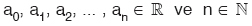olmak üzere,

P(x) = a₀ + a₁ × x + a₂ × x² + … + a_n × xⁿ

biçimindeki ifadelere x değişkenine göre, düzenlenmiş reel kat sayılı polinom (çok terimli) denir.

Burada, a₀, a₁, a₂, … a_n reel sayılarına polinomun kat sayıları,

a₀, a₁ × x , a₂ × x² , … , a_n × xⁿ ifadelerine polinomun terimleri denir.

a_n × xⁿ terimindeki a_n sayısına terimin kat sayısı, x in kuvveti olan
n sayısına terimin derecesi denir.

Derecesi en büyük olan terimin derecesine polinomun derecesi denir ve der[P(x)] ile gösterilir. Derecesi en büyük olan terimin kat sayısına ise polinomun baş kat sayısı denir.

Polinomlar kat sayılarına göre adlandırılırlar. Kat sayıları reel sayı olan polinomlara reel kat sayılı polinom, kat sayıları rasyonel sayı olan polinomlara rasyonel kat sayılı polinom, kat sayıları tam sayı olan polinomlara tam kat sayılı polinom denir.

Tanım

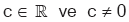olmak üzere, P(x) = c biçimindeki polinomlara, sabit polinom denir. Sabit polinomun derecesi 0 (sıfır) dır.

Tanım

P(x) = 0 biçimindeki polinoma, sıfır polinomu denir. Sıfır polinomunun derecesi tanımsızdır.

Polinomların Eşitliği

Aynı dereceli terimlerinin kat sayıları eşit olan polinomlar eşittir.

B. POLİNOMLARDA İŞLEMLER

1. Toplama İşlemi

İki polinom toplanırken; dereceleri aynı olan terimlerin kat sayıları kendi aralarında toplanır, sonuç o terimin kat sayısı olarak yazılır.

2. Çıkarma İşlemi

P(x) – Q(x) = P(x) + [–Q(x)]

olduğu için, P(x) polinomundan Q(x) polinomunu çıkarmak, P(x) ile
–Q(x) i toplamaktır. Bunun için çıkarma işlemini, çıkarılacak polinomun işaretini değiştirip toplama yapmak biçiminde ele alabiliriz.

3. Çarpma İşlemi

İki polinomun çarpımı; polinomlardan birinin her teriminin diğer polinomun her bir terimi ile ayrı ayrı çarpımlarından elde edilen terimler toplamınarak yapılır.

4. Bölme İşleminin Yapılışı

Polinomlarda bölme işlemi, sayılarda bölme işlemine benzer şekilde yapılır. Bunun için sırasıyla aşağıdaki işlemler yapılır:

1) Bölünen ve bölen polinomlar x değişkeninin azalan kuvvetlerine göre sıralanır.

2) Bölünen polinomun soldan ilk terimi, bölen polinomun soldan ilk terimine bölünür. Çıkan sonuç, bölümün ilk terimi olarak yazılır.

3) Bulunan bu bölüm, bölen polinomun bütün terimleri ile çarpılarak, aynı dereceli terimler alt alta gelecek şekilde bölünen polinomun altına yazılır.

4) Bölünenin altına yazılan çarpım polinomu, bölünen polinomdan çıkarılır.

5) Yukarıdaki işlemlere, kalan polinomun derecesi, bölen polinomun derecesinden küçük oluncaya kadar devam edilir.

Tanım

m > n olmak üzere, der[P(x)] = m ve der[Q(x)] = n olsun. P(x) in Q(x) ile bölümünden elde edilen bölüm polinomu B(x) olsun. Buna göre, der[P(x) + Q(x)] = m, der[P(x) – Q(x)] = m, der[P(x) × Q(x)] = m + n, der[B(x)] = m – n, der[[P(x)]k] = k × der[P(x)] = k × m, der[[P(xk)]] = k × der[P(x)] = k × m dir.

C. P(x) İN x = k İÇİN DEĞERİ

P(x) = a₀ + a₁ × x + a₂ × x² + … + a_n × xⁿ

polinomunun x = k için değeri,

P(k) = a₀ + a₁ × k + a₂ × k² + … +a_n × kⁿ dir.

Kural

P(x) = a0 + a1 × x + a2 × x2 + … + an × xn polinomunda x = 1 yazılırsa, P(1) = a0 + a1 + a2 + … + an olur. Bu durumda P(1) in değeri P(x) polinomunun kat sayıları toplamıdır.

Sonuç

Herhangi bir polinomda x yerine 1 yazılırsa, o polinomun kat sayıları toplamı bulunur. Örneğin, P(x + 7) polinomunun kat sayıları toplamı, P(1 + 7) = P(8) dir.

Kural

P(x) = a0 + a1 × x + a2 × x2 + … + an × xn polinomunda x = 0 yazılırsa, P(0) = a0 olur. Bu durumda P(0) ın değeri P(x) polinomunun sabit terimidir.

Sonuç

Herhangi bir polinomda x yerine 0 yazılırsa, o polinomun sabit (x ten bağımsız) terimi bulunur. Örneğin, P(2x + 3) polinomunun sabit terimi, P(0 + 3) = P(3) tür.

D. P(x) İN (ax + b) İLE BÖLÜNMESİYLE ELDE EDİLEN KALAN

P(x) in ax + b ile bölünmesiyle elde edilen bölüm B(x), kalan K olsun. Buna göre,

Yani; P(x) polinomunun ax + b ile bölünmesiyle elde edilen kalanı bulmak için, ax + b = 0 denkleminin kökü olan için P(x) polinomunun değeri olan hesaplanır.

Sonuç

P(x) polinomunun x – a ile bölümünden kalan P(a) dır. P(x + b) polinomunun x – a ile bölümünden kalan P(a + b) dir. P(3x + b) polinomunun x – a ile bölümünden kalan P(3 × a + b) dir.

E. P(x) İN xⁿ + a İLE BÖLÜMÜNDEN KALAN

Kural

Derecesi n den büyük olan bir polinomun xn + a ile bölümünden kalanı bulmak için, xn yerine –a yazılır. (xn + a = 0 ise, xn = –a)

F. P(x) İN (x – a) × (x – b) ÇARPIMI İLE BÖLÜNMESİ

Kural

1) P(x) polinomu (x – a) × (x – b) çarpımı ile tam olarak bölünebiliyorsa x – a ve x – b çarpanları ile de ayrı ayrı tam olarak bölünür. 2) x – a ve x – b aralarında asal polinomlar olmak üzere; P(x), bu polinomlara ayrı ayrı tam olarak bölünebiliyorsa, (x – a) × (x – b) çarpımı ile de tam olarak bölünür.

G. P(x) İN (a × x + b)² İLE BÖLÜNEBİLMESİ

P(x) polinomu (ax + b)² ile tam bölünebiliyorsa,

P(x) polinomu ve P'(x) polinomu ax + b ye tam olarak bölünür.
(P'(x), P(x) in türevidir.)

Buna göre, P(x) polinomu (ax + b)² ile tam bölünebiliyorsa,