KARTEZYEN ÇARPIM BAĞINTI
A. SIRALI n Lİ
n tane nesnenin belli bir öncelik sırasına göre düzenlenip, tek bir nesne gibi düşünülmesiyle elde edilen ifadeye sıralı n li denir.
(a, b) sıralı ikilisinde;
a ya birinci bileşen, b ye ikinci bileşen denir.
| a ¹ b ise, (a, b) ¹ (b, a) dır.
(a, b) = (c, d) ise, (a = c ve b = d) dir. |
B. KARTEZYEN ÇARPIM
A ve B herhangi iki küme olmak üzere, birinci bileşeni A kümesinden, ikinci bileşeni B kümesinden alınarak oluşturulan bütün sıralı ikililerin kümesine, A ile B nin kartezyen çarpımı denir.
A kartezyen çarpım B kümesi A ´ B ile gösterilir.
A ´ B = {(x, y) : x Î A ve y Î B} dir.
| A ¹ B ise, A ´ B ¹ B ´ A dır. |
C. KARTEZYEN ÇARPIMIN ÖZELİKLERİ
- 1) s(A) = m ve s(B) = n ise
s(A ´ B) = s(B ´ A) = m × n dir.
- A ´ (B ´ C) = (A ´ B) ´ C
- A ´ (B È C) = (A ´ B) È (A ´ C)
- (B È C) ´ A = (B ´ A) È (C ´ A)
- A ´ (B Ç C) = (A ´ B) Ç (A ´ C)
- (B Ç C) ´ A = (B ´ A) Ç (C ´ A)
- A ´ Æ = Æ ´ A = Æ
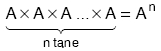
D. BAĞINTI
A ve B herhangi iki küme olmak üzere A ´ B nin her alt kümesine A dan B ye bağıntı denir.
Bağıntı genellikle b ile gösterilir.
b Ì A ´ B ise, b = {(x, y) : (x, y) Î A ´ B} dir.
| Ü | s(A) = m ve s(B) = n ise,
A dan B ye 2m×n tane bağıntı tanımlanabilir. |
| Ü | A ´ A nın herhangi bir alt kümesine A dan A ya bağıntı ya da A da bağıntı denir. |
| Ü | s(A) = m ve s(B) = n olmak üzere,
A dan B ye tanımlanabilen r elemanlı (r £ m × n) bağıntı sayısı
|
| Ü | b Ì A ´ B olmak üzere,
b = {(x, y) : (x, y) Î A ´ B} bağıntısının tersi b–1 Ì B ´ A dır. Buna göre, b bağıntısının tersi b–1 = {(y, x) : (x, y) Î b} dır. |
E. BAĞINTININ ÖZELİKLERİ
b, A da tanımlı bir bağıntı olsun.
1. Yansıma Özeliği
A kümesinin bütün x elemanları için (x, x) Î b ise, b yansıyandır.
“x Î A için, (x, x) Î b ise, b yansıyandır. (” : Her)
2. Simetri Özeliği
b bağıntısının bütün (x, y) elemanları için (y, x) Î b ise, b simetriktir.
“(x, y) Î b için (y, x) Î b ise, b simetriktir.
| Ü | b bağıntısı simetrik ise b = b–1 dir. |
| Ü | s(A) = n olmak üzere, A kümesinde tanımlanabilecek simetrik bağıntı sayısı  dir. |
| Ü | s(A) = n olmak üzere, A kümesinde tanımlanabilecek yansıyan bağıntı sayısı dir. |
3. Ters Simetri Özeliği
b bağıntısı A kümesinde tanımlı olsun.
x ¹ y iken “(x, y) Î b için (y, x) Ï b ise, b ters simetriktir.
| b bağıntısında (x, x) elemanın bulunması ters simetri özeliğini bozmaz. |
4. Geçişme Özeliği
b, A da tanımlı bir bağıntı olsun.
“[(x, y) Î b ve (y, z) Î b] için (x, z) Î b ise,
b bağıntısının geçişme özeliği vardır.
| Boş kümeden farklı bir A kümesinde tanımlanan b = Æ bağıntısında yansıma özeliği yoktur. Simetri, Ters simetri, geçişme özeliği vardır. |
F. BAĞINTI ÇEŞİTLERİ
1. Denklik Bağıntısı
b bağıntısı A kümesinde tanımlı olsun.
b; Yansıma, Simetri, Geçişme özeliğini sağlıyorsa denklik bağıntısıdır.
| Ü | b, A kümesinde tanımlı bir denklik bağıntısı olsun. (x, y) Î b ise x ve y elemanları b bağıntısına göre denktir denir ve x º y şeklinde yazılır. |
| Ü | b, A kümesinde tanımlı bir denklik bağıntısı olsun. A da x elemanına denk olan bütün elemanların kümesine x in denklik sınıfı denir ve şeklinde gösterilir. x in denklik sınıfının kümesi,
|
2. Sıralama Bağıntısı
A kümesinde tanımlı b bağıntısında; Yansıma, Ters simetri, Geçişme özeliği varsa b sıralama bağıntısıdır.
| Bir bağıntı hem denklik, hem de sıralama bağıntısı olabilir. |
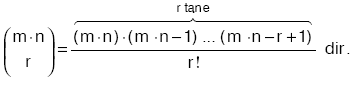
Hemen Yorum Yaz