FONKSİYON
A. TANIM
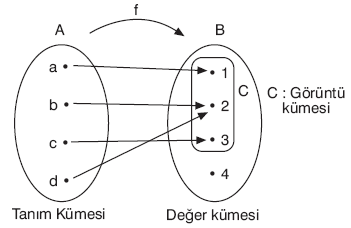
A ¹ Æ ve B ¹ Æ olmak üzere, A dan B ye bir b bağıntısı verilmiş olsun.
A nın her elemanı B nin elemanlarıyla en az bir kez ve en çok bir kez eşleniyorsa bu bağıntıya fonksiyon denir.
“x Î A ve y Î B olmak üzere, A dan B ye bir f fonksiyonu
f : A ® B ya da x ® f(x) = y biçiminde gösterilir. A ya fonksiyonun tanım kümesi, B ye de değer kümesi denir.
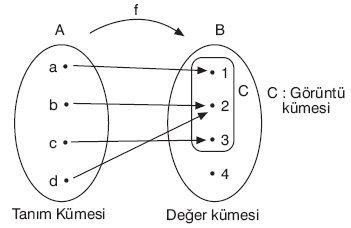
Yukarıda A dan B ye tanımlanan f fonksiyonu
f = {(a, 1), (b, 2), (c, 3), (d, 2)}
biçiminde de gösterilir.
| Ü | Her fonksiyon bir bağıntıdır. Fakat her bağıntı fonksiyon olmayabilir. |
| Ü | Görüntü kümesi değer kümesinin alt kümesidir. |
| Ü | s(A) = m ve s(B) = n olmak üzere,
i) A dan B ye nm tane fonksiyon tanımlanabilir. ii) B den A ya mn tane fonksiyon tanımlanabilir. iii) A dan B ye tanımlanabilen fonksiyon olmayan bağıntıların sayısı 2m × n – nm dir. |
| Ü | Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için, y eksenine paralel doğrular çizilir. Bu doğrular fonksiyonun belirttiği eğride en az bir ve en çok bir noktayı kesiyorsa verilen bağıntı x ten y ye bir fonksiyondur. |
B. FONKSİYONLARDA İŞLEMLER
A Ç B ¹ Æ olmak üzere,
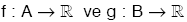 fonksiyonları tanımlansın.
fonksiyonları tanımlansın.
- (f + g) : A Ç B ®
 , (f + g)(x) = f(x) + g(x)
, (f + g)(x) = f(x) + g(x) - (f – g) : A Ç B ®
 , (f – g)(x) = f(x) – g(x)
, (f – g)(x) = f(x) – g(x) - (f × g) : A Ç B ®
 , (f × g)(x) = f(x) × g(x)
, (f × g)(x) = f(x) × g(x) - “x Î A Ç B için, g(x) ¹ 0 olmak üzere,
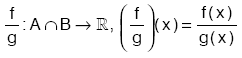
- c Î
 olmak üzere,
olmak üzere,
(c × f) : A ®
 , (c × f)(x) = c × f(x) tir.
, (c × f)(x) = c × f(x) tir.
C. FONKSİYON ÇEŞİTLERİ
1. Bire Bir Fonksiyon
Bir fonksiyonda farklı elemanların görüntüleri de farklıysa fonksiyon bire birdir..
BBuna göre, bire bir fonksiyonda,
“x1, x2 Î A için, x1 ¹ x2 iken f(x1) ¹ f(x2) olur.
Diğer bir ifadeyle,
“x1, x2 Î A için, f(x1) = f(x2) iken
x1 = x2 ise, f fonksiyonu bire birdir.
| Ü | s(A) = m ve s(B) = n (n ³ m) olmak üzere,
A dan B ye tanımlanabilecek bire bir fonksiyonların sayısı,
|
2. Örten Fonksiyon
Görüntü kümesi değer kümesine eşit olan fonksiyonlara örten fonksiyon denir.
| Ü | f : A ® B
f(A) = B ise, f örtendir. |
| Ü | s(A) = m olmak üzere, A dan A ya tanımlanabilen bire bir örten fonksiyonların sayısı,
m! = m × (m – 1) × (m – 2) × … × 3 × 2 × 1 dir. |
3. İçine Fonksiyon
Örten olmayan fonksiyona içine fonksiyon denir.
| Ü | İçine fonksiyonun değer kümesinde eşlenmemiş eleman vardır. |
| Ü | s(A) = m olmak üzere, A dan A ya tanımlanabilen içine fonksiyonların sayısı mm – m! dir. |
4. Birim (Etkisiz) Fonksiyon
Her elemanı kendisine eşleyen fonksiyona birim fonksiyon denir.
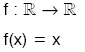
ise, f birim (etkisiz) fonksiyondur.
| Ü | Birim fonksiyon genellikle I ile gösterilir. |
5. Sabit Fonksiyon
Tanım kümesindeki bütün elemanları değer küme-sindeki bir elemana eşleyen fonksiyona sabit fonksiyon denir.
| Ü | “x Î A ve c Î B için,
f : A ® B f(x) = c ise, f sabit fonksiyondur. |
| Ü | s(A) = m, s(B) = n olmak üzere,
A dan B ye n tane sabit fonksiyon tanımlanabilir. |
6. Çift ve Tek Fonksiyon
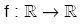
f(–x) = f(x) ise, f fonksiyonu çift fonksiyondur.
f(–x) = –f(x) ise, f fonksiyonu tek fonksiyondur.
| Ü | Çift fonksiyonların grafikleri Oy eksenine göre simetriktir. |
| Ü | Tek fonksiyonların grafikleri orijine göre simetriktir. |
D. EŞİT FONKSİYON
f : A ® B
g : A ® B
Her x Î A için f(x) = g(x) ise, f fonksiyonu g fonksiyonuna eşittir.
E. PERMÜTASYON FONKSİYON
f : A ® A
olmak üzere, f fonksiyonu bire bir ve örten ise, f fonksiyonuna permütasyon fonksiyon denir.
A = {a, b, c} olmak üzere, f : A ® A
f = {(a, b), (b, c), (c, a)}
fonksiyonu permütasyon fonksiyon olup
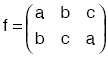 biçiminde gösterilir.
biçiminde gösterilir.
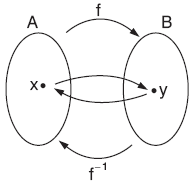
F. TERS FONKSİYON
f : A ® B, f = {(x, y)|x Î A, y Î B} bire bir ve örten fonksiyon olmak üzere,
f–1 : B ® A, f–1 = {(y, x)|(x, y) Î f} fonksiyonuna f nin ters fonksiyonu denir.
 |
(x, y) Î f ise, (y, x) Î f–1 olduğu için,
y = f(x) ise, x = f–1(y) dir. Ayrıca, (f–1)–1 = f dir. |
| (f–1)–1 = f dir. Ancak, (f–1(x))–1 ¹ f(x) tir. |
| f fonksiyonu bire bir ve örten değilse, f–1 fonksiyon değildir. |
| f : A ® B ise, f–1 : B ® A olduğu için, f nin tanım kümesi, f–1 in değer kümesidir. f nin değer kümesi de, f–1 in tanım kümesidir. |
| f(a) = b ise, f–1(b) = a dır.
f–1(b) = a ise, f(a) = b dir. |
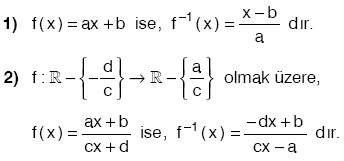 |
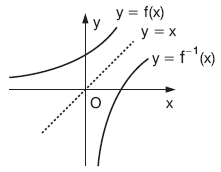
| Ü | y = f(x) fonksiyonunun grafiği ile y = f–1(x) in grafiği y = x doğrusuna göre birbirinin simetriğidir.
|
| Ü | 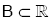 olmak üzere, olmak üzere,
|
| Ü | 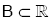 olmak üzere, olmak üzere,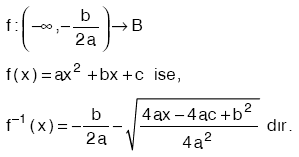 |
G. BİLEŞKE FONKSİYON
f : A ® B, g : B ® C fonksiyonları tanımlansın.
f ve g yi kullanarak A kümesinin elemanlarını C kümesinin elemanlarına eşleyen fonksiyona g ile f nin bileşke fonksiyonu denir.
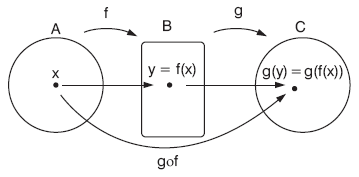
Buna göre,
f : A ® B ve g : B ® C olmak üzere, gof : A ® C fonksiyonuna f ile g nin bileşke fonksiyonu denir ve g bileşke f diye okunur.
| Ü | (gof)(x) = g[f(x)] tir. |
| Bileşke işleminin değişme özeliği yoktur.
Bu durumda, fog ¹ gof dir. Bazı fonksiyonlar için fog = gof olabilir. Ancak bu “fonksiyonlarda değişme özeliği yoktur.” gerçeğini değiştirmez. |
| Ü | Fonksiyonlarda bileşke işleminin birleşme özeliği vardır.
Bu durumda (fog)oh = fo(goh) = fogoh olur. |
| Ü | I birim fonksiyon olmak üzere,
foI = Iof = f ve f–1of = fof–1 = I dır. |
| Ü | f, g ve h fonksiyonları bire bir ve örten olmak üzere,
(fog)–1 = g–1of–1 ve (fogoh)–1 = h–1og–1of–1 dir. |
| Ü | (fog)(x) = h(x)
ise, f(x) = (hog–1)(x) dir. ise, g(x) = (f–1oh)(x) tir. |
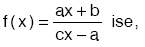
• f–1 (x) = f(x) tir. • (fof) (x) = x • (fofof) (x) = f(x) • (fofofof) (x) = x … |
H. FONKSİYONUN GRAFİĞİ
Bir fonksiyonun elemanlarına analitik düzlemde karşılık gelen noktaların kümesine bu fonksiyonun grafiği denir.
f : A ® B, f = {(x, y)|x Î A, y Î B, y = f(x)}
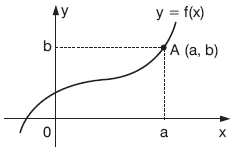 |
(a, b) Î f
olduğundan f(a) = b dir. Ayrıca, f–1(b) = a dır. |
| Ü | 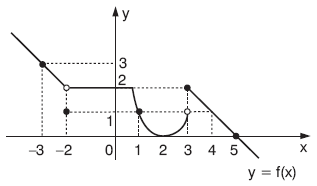
Yukarıdaki y = f(x) fonksiyonunun grafiğine göre, f(–3) = 3, f(–2) = 1, f(–1) = 2, f(0) = 2, f(1) = 1, f(2) = 0, f(3) = 2, f(4) = 1, f(5) = 0 dır. |
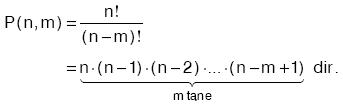
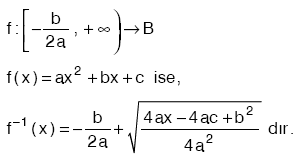






Bir yanıt yazın