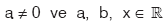
EŞİTSİZLİKLER
A. BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
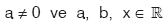olmak üzere,
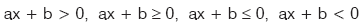
şeklindeki ifadelere birinci dereceden bir bilinmeyenli eşitsizlik adı verilir. Eşitsizliği çözmek için f(x) = ax + b fonksiyonunun tablosu yapılır. Eşitsizliği sağlayan aralık bulunur.
f(x) = ax + b fonksiyonunun işaret tablosu aşağıda verilmiştir.
ax + b = 0 denkleminin kökü 
dır.
B. KISA YOLDAN FONKSİYONUN İŞARETİNİN İNCELENMESİ
Kısalığından dolayı bütün eşitsizliklerin çözüm yolunu kolayca bulabileceğiniz bir yaklaşım vereceğiz.
f(x), çarpım veya bölüm fonksiyonu olsun.
Tablo oluştururken sırasıyla şu işlemler yapılır:
1) f(x) in payı ile paydasını sıfır yapan değerler bulunup sırasıyla tabloya yazılır.
2) (Eşitsizliğin tanımı gözönüne alınarak) pay ile paydayı sıfır yapan değerlerden tek sayıda olanlarına tek katlı kök, çift sayıda olanlarına çift katlı kök denir.
3) Her bileşenin en büyük dereceli terimlerinin işaretleri çarpılarak veya bölünerek f(x) in işareti bulunur.
4) Tablodaki en büyük kökün sağındaki kutuya f(x) in işareti yazılır.
5) Tek katlı köklerin soluna sağındaki işaretinin tersi, çift katlı köklerin soluna sağındaki işaretin aynısı yazılır.
Kural
| ax2 + bx + c > 0 eşitsizliğinin çözüm kümesi, ise, (a > 0 ve D = b2 – 4ac < 0) dır.
|
Uyarı
|
gibi eşitsizliklerin çözüm kümesi bulunurken, içler dışlar çarpımı yapılamaz. Çünkü paydadaki f(x), h(x) ve m(x) in pozitif ya da negatif olduğunu bilmiyoruz. |
Uyarı
|
gibi eşitsizliklerin çözüm kümesi bulunurken, g(x) = 0 ın kökleri kesri tanımsız yapacağından çözüm kümesine dahil edilmez. |
C. İKİNCİ DERECEDEN DENKLEMLERİN KÖKLERİNİN İŞARETLERİNİN İNCELENMESİ
ax2 + bx +c = 0 denkleminin köklerinin varlığını D, köklerinin işaretini belirler.
a × c < 0 ise denklemin farklı iki reel kökü vardır.
a × c > 0 ise denklemin denklemin köklerinin varlığı ile ilgili kesin bir şey söylenemez.
ax2 + bx + c = 0 denkleminin kökleri x1 ve x2 olsun.
Zıt işaretli köklerin olması için, olmalıdır.
(x1 < 0 < x2 ve |x1| > x2) olması için, olmalıdır.
(x1 < 0 < x2 ve |x1| < x2) olması için, olmalıdır.
Köklerin aynı işaretli olması için, olmalıdır.
0 < x1 < x2 olması için, olmalıdır.
x1 < x2 < 0 olması için, olmalıdır.
hayatım 7/12 sadece matamatik yani kardeş sayılırız çünkü, kendimden çok matamatiki görüyorum bi aynı anneden doğmadık
keşke biraz da türkçe görsen. :)
0 Çakacam :D
Bune kardeşim ben denklem ve eşitsizlik konu anlatımı yazdım bu çıktı :D
bu bilgiler çok yetersiz:(
çok yardımcı oldunuz teşekkrler. bu matematikten çektiğimizi hayattan çekmemişizdir
Çok haklısın kardeşim ?
Dans ederken cep telefonumdanda bu konuları çalışıyorum çok şanlı çok tatlıyım yaşım daha 12.5 :)
Bebe 12,5 yasında eşitsizlikmi çalışıyon
12.5 :D :D Allah kurtarsın kardeşim :D
Bebe sen sus :D
12,5 yaşındaki bebe ay kıyamam sana sen çokmu zekisin ekmek(mama)yenmi.
kardeşim 16 yaşındayım ben senle dalga geçsem nasıl düşünürsün ??? ayıp ama aaa ben lise 1 sen ortaokul 8 mi ha
lise birdeysen on dört yaşındasın yuh nerden salladın 16 yı yaş hesaplama yaz bak yaşına akıllı
16 sın lise1 iyiymiş ben 17 lise 3
bune yaaaaa çok karışık nedir bu matematikten çektiğimiz
Çok güzel harika bilgiler Teşekkürler
Umarim ise yarar güzel birşey
bu bilgiler çok az soru çözmem için daha fazlasına ihtiyacım var ama olsun zekam sayesinde hepsini çözerim
teşekkürler süperdi harikasınız
süperrrr çok güzel yardımcı olduğunuz için teşekkür
bende yardımcı olabilirim
tesekkurler sagolun bilgiler için :)
gençler çalışın bunları yaparsınız
Lütfen cevap verir misiniz ?
birinci dereceden bir bilinmeyenli eşitsizliklerin çözüm kümesinde işaretlri nasıl buluyorduk ?
Yazdım kötü not almam ınş
burda çok az bilgi var eşitsizlik sorusu çözebilmek için çok daha detaylı anlatılmalı
çok thank you dostlar :)
fazla ıyı degıl ama yınede napalım baska sıte yok
Bizim Dönem Ödevi….
Birbirinden farklı iki pozitif kök var diyo nasıl bulabilirim?
teşekkürler :D
daha yok mu bizim mat . öğrt. 7 sayfa yazı istiyo performans ödevinee
arkdaşlar yazdım perşembe günü hocaya teslim etcem ,inşallah iyi not alırım alamassam varya
D delta demek
D delta demeek
delta=b(kare)-4.a.c
katılıyorum ÖĞRENCİYE
x1 < x2 0 ve D = b2 – 4ac < 0) dır. ifadesin de &guot;D&guot; nin anlamı nedir ACELE cevap verirseniz sevinirim…
teşekkürler şimdiden