Trigonometri 1 Konu Anlatımı ve Ders Notları

TRİGONOMETRİ 1

I. AÇI, YÖNLÜ AÇI, YÖNLÜ YAY

A. AÇI

Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir.

B. YÖNLÜ AÇI

Bir açının kenarlarından birini, başlangıç kenarı; diğerini bitim kenarı olarak aldığımızda elde edilen açıya yönlü açı denir.

Açılar adlandırılırken önce başlangıç, sonra bitim kenarı yazılır.

Kural

Açının köşesi etrafında, başlangıç kenarından bitim kenarına iki türlü gidilebilir. Bunlardan biri saatin dönme yönünün tersi, ikincisi ise saatin dönme yönünün aynısıdır. Saatin dönme yönünün; tersi olan yöne pozitif yön, aynı olan yöne negatif yön denir. Açıların yönü ok yardımıyla belirlenir.

C. YÖNLÜ YAYLAR

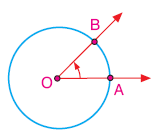O merkezli çemberde ile bu açının iç bölgesindeki noktaların kümesinin O merkezli çemberle kesişimi AB yayıdır. AB yayı, biçiminde gösterilir.

nın yönü olarak, AOB açısının yönü alınır. Şekildeki AOB açısının yönü pozitif olduğundan, da pozitif yönlüdür.

Pozitif yönlü AB yayında A ya yayın başlangıç noktası, B ye yayın bitim noktası denir.

D. BİRİM ÇEMBER

Analitik düzlemde merkezi O(0, 0) (orijin) ve yarıçapı 1 birim olan çembere birim (trigonometrik) çember denir.

Birim çemberin denklemi: x2 + y2 = 1 dir.

E. AÇI ÖLÇÜ BİRİMLERİ

Bir açının ölçüsünün büyüklüğünü veya küçüklüğünü tanımlamak için, bir ölçü birimi tanımlanmalıdır. Açıyı ölçmek, açının kolları arasındaki açıklığı belirlemek demektir.

Genellikle iki birim kullanılır. Bunlar; derece ve radyandır.

1. Derece

Bir tam çember yayının 360 eş parçasından birini gören merkez açının ölçüsüne 1 derece denir. Ve 1° ile gösterilir.

2. Radyan

Yarıçap uzunluğuna eşit uzunluktaki bir yayı gören merkez açının ölçüsüne 1 radyan denir.

Uyarı

Birim çemberin çevresi 360° veya 2p radyan olduğu için, 360° = 2p radyan dır.

Kural

Derece D ile radyan R ile gösterilirse,

F. ESAS ÖLÇÜ

olmak üzere, birim çember üzerinde a açısı ile
a + k × 360° açısı aynı noktaya karşılık gelmektedir. Buna göre,

olmak üzere, ölçüsü

a + k × 360°

olan açının esas ölçüsü a derecedir.

Açının birimi ne olursa olsun, esas ölçü negatif yönlü olamaz. Diğer bir ifadeyle esas ölçü [0°, 360°) aralığındadır.

Derece cinsinden verilen pozitif açılarda, açı 360° ye bölünür. Elde edilen kalan esas ölçüdür.

Derece cinsinden verilen negatif yönlü açılarda, açının mutlak değeri 360° ye bölünür; kalan 360° den çıkarılarak esas ölçü bulunur.

Radyan cinsinden verilen açılarda açının içerisinden 2p nin katları atılır. Geriye kalan esas ölçüdür.

Radyan cinsinden verilen negatif yönlü açıların esas ölçüsü bulunurken, verilen açı pozitif yönlü açı gibi düşünülerek esas ölçü bulunur. Bulunan değer 2p den çıkarılır.

nin esas ölçüsü aşağıdaki yolla da bulunabilir. a sayısı b nin 2 katına bölünür. Kalan p nin kat sayısı olarak paya yazılır payda aynen yazılır.
a nın b nin 2 katına bölümünden kalan k ise nin esas ölçüsü dir.

II. TRİGONOMETRİK FONKSİYONLAR

A. KOSİNÜS FONKSİYONU

Bir x reel sayısını cosx e dönüştüren fonksiyona kosinüs fonksiyonu denir.

Birim çember üzerinde P(x, y) noktası ile eşlenen açı olmak üzere, P noktasının apsisine, a reel (gerçel) sayısının kosinüsü denir ve cosa ile gösterilir.

x = cosa dır. Kosinüs fonksiyonunun görüntü kümesi (aralığı), [–1, 1] dir. Yani, her için, –1 £ cosa £ 1 dir.

B. SİNÜS FONKSİYONU

Bir x reel sayısını sinx e dönüştüren fonksiyona sinüs fonksiyonu denir.

Birim çember üzerinde P(x, y) noktası ile eşlenen açı olsun. P noktasının ordinatına, a reel (gerçel) sayısının sinüsü denir ve sina ile gösterilir.

y = sina Sinüs fonksiyonunun görüntü kümesi (aralığı), [–1, 1] dir. Yani, her için, –1 £ sina £ 1 dir.

Sonuç

Şekilde, A(1, 0) olduğundan, cos0° = 1 ve sin0° = 0 dır. B(0, 1) olduğundan, cos90° = 0 ve sin90° = 1 dir. C(–1, 0) olduğundan, cos180° = –1 ve sin180° = 0 dır. D(0, –1) olduğundan, cos270° = 0 ve sin270° = –1 dir.

Kural

Şekilde, x = cosa, y = sina |OK| = sina ve |OH| = cosa olduğuna göre, OHP dik üçgeninde; |OH|2 + |PH|2 = 12 cos2a + sin2a = 1 dir.

C. TANJANT FONKSİYONU

Birim çember üzerinde P(x, y) noktası ile eşlenen açı olsun. [OP nın x = 1 doğrusunu kestiği T noktasının ordinatına, a reel (gerçel) sayısının tanjantı denir ve tana ile gösterilir.

x = 1 doğrusuna tanjant ekseni denir.

t = tana dır.

D. KOTANJANT FONKSİYONU

Birim çember üzerinde P(x, y) noktası ile eşlenen açı olsun. [OP nın y = 1 doğrusunu kestiği K noktasının apsisine, a reel (gerçel) sayısının kotanjantı denir ve cota ile gösterilir.

y = 1 doğrusuna kotanjant ekseni denir.

c = cota

Sonuç

(T.sız: Tanımsız)

Koordinat Sisteminde, Birim Çemberdeki Dört Bölgeye Göre Kosinüs ve Sinüs Fonksiyonlarının İşaretleri

Kural

Uyarı

cosa nın işaretinin sina nın işaretine bölümü cota nın işaretini; sina nın işaretinin cosa nın işaretine bölümü tana nın işaretini verir. 4 bölgede de tana ile cota nın işareti aynıdır.

E. KOSEKANT, SEKANT FONKSİYONU

Birim çember üzerinde olmak üzere,

P noktasındaki teğetin y eksenini kestiği noktanın ordinatına, a reel (gerçel) sayısının kosekantı denir ve csca ile ya da coseca gösterilir.

P noktasındaki teğetin x eksenini kestiği noktanın apsisine, a reel (gerçel) sayısının sekantı denir ve seca ile gösterilir.

c = coseca s = seca

Kural

Sonuç

cosecx ve secx in sonucu (–1, 1) aralığındaki sayılara eşit olamaz. 1 + tan2x = sec2x 1 + cot2x = cosec2x

F. DİK ÜÇGENDE DAR AÇILARIN TRİGONOMETRİK ORANLARI

BCA dik üçgeninde, aşağıdaki eşitlikleri yazabiliriz.

Sonuç

Ölçüleri toplamı 90° olan (tümler) iki açıdan birinin sinüsü, diğerinin kosinüsüne; birinin tanjantı, diğerinin kotanjantına; birinin sekantı, diğerinin kosekantına eşittir. Buna göre, Bazı dar açıların trigonometrik değerleri aşağıda verilmiştir. Bu değerlerin çok iyi bilinmesi soruları daha hızlı çözmenizi sağlar.

Kural

x açısı; dar açı olarak kabul edilmek üzere, trigonometrik değerin hangi bölgede olduğu bulunur. Daha sonra, fonksiyonun o bölgedeki işareti belirlenir. Eşitliğin iki tarafında fonksiyonların adı aynı olur.

Kural

x açısı; dar açı olarak kabul edilmek üzere, trigonometrik değerin hangi bölgede olduğu bulunur. Daha sonra, fonksiyonun o bölgedeki işareti belirlenir. Eşitliğin iki tarafında fonksiyonların adı farklı olur. Bu farklılık, sinüs için kosinüs, kosinüs için sinüs, tanjant için kotanjant, kotanjant için de tanjanttır.

Kural