BÖLME ve BÖLÜNEBİLME
A. BÖLME
A, B, C, K birer doğal sayı ve B ¹ 0 olmak üzere,
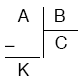
bölme işleminde,
- A ya bölünen, B ye bölen, C ye bölüm, K ya kalan denir.
- A = B × C + K dir.
- Kalan, bölenden küçüktür. (K < B)
- Kalan, bölümden (C den) küçük ise, bölen (B) ile bölümün (C) yeri değiştirilebilir. Bu durumda A ve K değişmez.
- K = 0 ise, A sayısı B ile tam bölünebilir.
B. BÖLÜNEBİLME KURALLARI
1. 2 İle Bölünebilme
Birler basamağındaki rakamı çift olan sayılar 2 ile tam bölünür.
Tek sayıların 2 ile bölümünden kalan 1 dir.
2. 3 İle Bölünebilme
Rakamlarının sayısal değerleri toplamı 3 ün katı olan sayılar 3 ile tam bölünür.
Bir sayının 3 ile bölümünden kalan, rakamlarının toplamının 3 ile bölümünden kalana eşittir.
3. 4 İle Bölünebilme
Bir sayının onlar basamağındaki rakam ile birler basamağındaki rakamın (son iki basamak) belirttiği sayı, 4 ün katı olan sayılar 4 ile tam bölünür.
… abc sayısının 4 ile bölümünden kalan bc nin (son iki basamak) 4 ile bölümünden kalana eşittir.
- … abc sayısının 4 ile bölümünden kalan
c + 2 . b nin 4 ile bölümünden kalana eşittir.
4. 5 İle Bölünebilme
Birler basamağındaki rakam 0 veya 5 olan sayılar 5 ile tam bölünür.
Bir sayının 5 ile bölümünden kalan, o sayının birler basamağındaki rakamın 5 ile bölümünden kalana eşittir.
5. 7 İle Bölünebilme
(n + 1) basamaklı anan-1 … a4a3a2a1a0 sayısının 7 ile tam bölünebilmesi için,
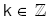 olmak üzere,
olmak üzere,
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) +…– … = 7k
olmalıdır.
| Ü | Birler basamağı a0, onlar basamağı a1, yüzler basamağı a2, … olan sayının (…a5 a4 a3 a2 a1 a0 sayısının) 7 ile bölümünden kalan
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) +…– … … işleminin sonucunun 7 ile bölümünden kalana eşittir. |
| Sekiz basamaklı ABCDEFGH sayısının 7 ile bölümünden kalan,
(H + 3 × G + 2 × F) – (E + 3 × D + 2 × C) + (B + 3 × A) işleminin sonucunun 7 ile bölümünden kalandır. |
6. 8 İle Bölünebilme
Yüzler basamağındaki, onlar basamağındaki ve birler basamağındaki rakamların (son üç rakamın) belirttiği sayı 8 in katı olan sayılar 8 ile tam bölünür.
3000, 3432, 65104 sayıları 8 ile tam bölünür.
| Ü | Birler basamağı c, onlar basamağı b, yüzler basamağı a, … olan sayının (… abc sayısının) 8 ile bölümünden kalan c + 2 × b + 4 × a toplamının 8 ile bölümünden kalana eşittir. |
7. 9 İle Bölünebilme
Rakamlarının toplamı 9 un katı olan sayılar 9 ile tam bölünür.
Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalana eşittir.
8. 10 İle Bölünebilme
Birler basamağındaki rakamı 0 (sıfır) olan sayılar 10 ile tam bölünebilir. Bir sayının birler basamağındaki rakam o sayının 10 ile bölümünden kalandır.
9. 11 İle Bölünebilme
(n + 1) basamaklı anan–1 … a4a3a2a1a0 sayısının 11 ile tam bölünebilmesi için
(a0 + a2 + a4 + …) – (a1 + a3 + a5 + …)… = 11 . k
ve  olmalıdır.
olmalıdır.
| Ü | (n + 1) basamaklı anan–1 … a4a3a2a1a0 sayısının 11 ile bölümünden kalan
(a0 + a2 + a4 + …) – (a1 + a3 + a5 + …)… işleminin sonucunun 11 ile bölümünden kalana eşittir. |
Aralarında asal iki sayıya bölünebilen bir sayı, bu iki sayının çarpımına da tam bölünür.
|
|
C. BÖLEN KALAN İLİŞKİSİ
A, B, C, D, E, K1, K2 uygun koşullarda birer doğal sayı olmak üzere,
A nın C ile bölümünden kalan K1 ve
B nin C ile bölümünden kalan K2 olsun.
Buna göre,
- A × B nin C ile bölümünden kalan K1 × K2 dir.
- A + B nin C ile bölümünden kalan K1 + K2 dir.
- A – B nin C ile bölümünden kalan K1 – K2 dir.
- D × A nın C ile bölümünden kalan D × K1 dir.
- AE nin C ile bölümünden kalan (K1)E dir.
Yukarıdaki işlemlerde kalan değerler bölenden (C den) büyük ise, tekrar C ile bölünerek kalan bulunur.
D. ÇARPANLAR İLE BÖLÜM
Bir A doğal sayısı B × C ile tam bölünüyorsa A sayısı B ve C doğal sayılarıyla da bölünebilir. Fakat bu ifadenin karşıtı (A sayısı B ile ve C ile tam bölünüyorsa A sayısı B × C ile tam bölünür.) doğru olmayabilir.
- 144 sayısı 2 × 6 = 12 ile tam bölünür ve 144 sayısı 2 ile ve 6 ile de tam bölünür.
- 6 sayısı 2 ile ve 6 ile tam bölünür. Fakat 6 sayısı 2 × 6 = 12 ile tam bölünemez.
E. BİR TAM SAYININ TAM BÖLENLERİ
Bir tam sayının, asal çarpanlarının kuvvetlerinin çarpımı biçiminde yazılmasına bu sayının asal çarpanlarının kuvvetleri biçiminde yazılması denir.
a, b, c birbirinden farklı asal sayılar ve m, n, k pozitif tam sayılar olmak üzere,
A = am . bn . ck olsun.
Bu durumda aşağıdakileri söyleyebiliriz:
- A yı tam bölen asal sayılar a, b, c dir.
- A sayısının pozitif tam bölenlerinin sayısı,
(m + 1) × (n + 1) × (k + 1) dir.
- A sayısının pozitif tam bölenlerinin ters işaretlileri de negatif tam bölenidir.
- A sayısının tam sayı bölenleri sayısı,
2 × (m + 1) × (n + 1) × (k + 1) dir.
- A sayısının tam sayı bölenleri toplamı 0 (sıfır) dır.
- A sayısının pozitif tam bölenlerinin toplamı,

- A sayısının asal olmayan tam sayı bölenlerinin sayısı, A nın tam sayı bölenlerinin sayısından A nın asal bölenlerinin sayısı çıkarılarak bulunur.
- A nın asal olmayan tam sayı bölenleri toplamı,
– (a + b + c) dir.
- A sayısından küçük A ile aralarında asal olan doğal sayıların sayısı,

- A sayısının pozitif tam sayı bölenlerinin çarpımı:
çok güzel şeyler yazmışsınız konu formülleri süper.
çok güzel aşık oldum resmen yani
delimiyimki bu sayfaya girim deli şeyler,
yazılı anlatımıda böyle ben istemedim yani
33 basamaklı 333…….3333 sayısının 4 ile bölümünden kalan x ,5 ile bölümünden kalan y olduğuna göre x+y toplamı kaçtır tarzı soruların çözümü ?
33 son iki basamagı 4 ile bölümünden kalan 1 olur 4 e bölünebilme kuralına bakabilrisin , 5 e bölümünde son basamağı 3 kalanı da 3. 1+3=4
bölme konu anlatımı lazımdı formüller ve sınav öncesi tekrar için bire bir bu sayfa.